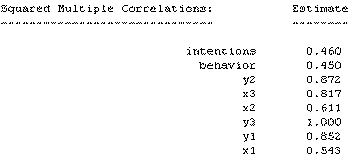Consequences of Measurement Error Application
Researchers in marketing and the social and behavioral sciences often work with theories that posit relationships between concepts. In Amos, the concepts are latent variables that are measured by one or more indicators using structural equation modeling (SEM). The measures are often imperfect and contain measurement error. Consequences of measurement error include:
- Attenuation of effect: the estimated effect is weaker than the real effect
- Inconsistency: consistency is a property of an estimator wherein as the sample size increases the estimate converges to the true value. A perhaps surprising consequence of measurement error is that error in any variable can adversely affect estimated parameters throughout the model.
In practice, researchers use reliable multiple indicators to try to overcome these problems. The following example illustrates how multiple indicators can help remedy measurement error.
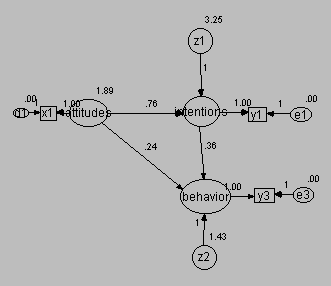
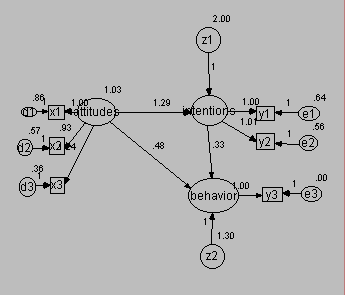
No provision for measurement error
In a study of coupon usage, Richard Bagozzi considers a model in which attitudes affect behavior both directly and by way of intentions. He compares models in which single and multiple indicators are used.
The model with no provision for measurement error appears in the following figure.
This path diagram illustrates the use of a single indicator to represent each latent variable:
- X1 is an indicator of attitudes
- Y1 is an indicator of intentions
- Y3 is an indicator of behavior
This model makes no provision for measurement error. The indicators are treated as perfect measures of their respective latent variables.
Amos produces the following regression estimates.
Click to View Larger Image
Note that these coefficients are un-standardized.
Amos produces the following variance estimates.
Click to View Larger Image
Finally, Amos produces the following estimates of R-square.
Click to View Larger Image
Note that to estimate the model you must set certain regression weights to 1 and certain variances to 0. These values appear in the Amos input model graphic shown above.
Here is Amos graphic output for the above model.
Measurement error taken into account in attitudes
This model appears in the following figure.
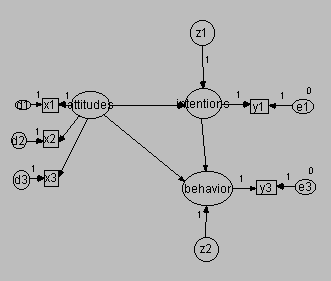
In this model, there are now three indicators of attitudes, namely, X1, X2, and X3. To make the model identified, you must fix the scale of attitudes. You can either set the variance of attitudes to a constant, or you can constrain one of the regression weights from attitudes to its indicators to 1. We did the latter in this instance.
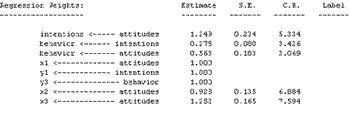
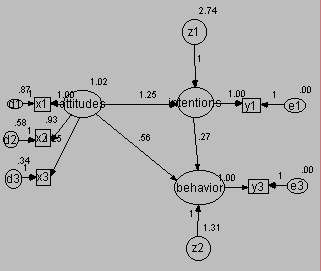
Amos produces the following regression weights for this model.
Click to View Larger Image
Note that the estimated impact of attitudes on intentions has increased by 64 percent from 0.76 to 1.25, and that the estimated impact of attitudes on behavior has more than doubled from 0.24 to 0.56. The impact of intentions on behavior has decreased slightly, from 0.36 to 0.28.
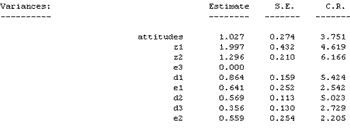
Amos produces the following variance estimates for this model.
Click to View Larger Image
Finally, Amos produces the following R-squared values.
Click to View Larger Image
The R-squared for intentions has increased from 0.252 to 0.369 while that for behavior has increased from 0.393 to 0.445. The squared multiple correlations for X1, X2, and X3 are 0.542, 0.603, and 0.825 respectively. Note that due to measurement error these values are not 1. Based upon these values, you might conclude that X3 is the most reliable indicator of attitudes.
Here is the estimated model in an Amos graphic.
Measurement error taken into account in both attitudes and intentions
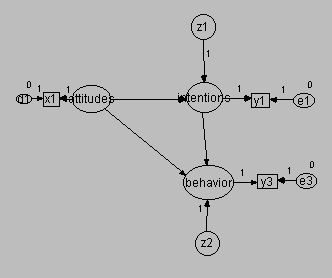
This model appears in the following figure.
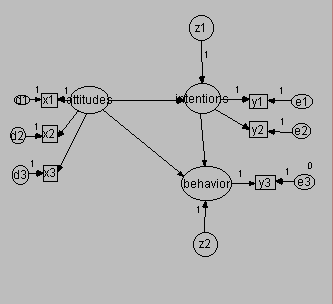
This model augments the previous model by adding a second indicator (Y2) for intentions. To make the model identified, you must specify a constraint: either fix the variance of intentions or set the regression weight for one of intentions' indicators to 1. Here, we did the latter.
Amos produces the following regression weights for this model.
Click to View Larger Image
Regarding the structural part of the model, the regression coefficients differ slightly from the second model above.
Amos produces the following variances for this model.
Click to View Larger Image
Finally, Amos produces the following R-square values.
Click to View Larger Image
The R-square for intentions improved from 0.369 to 0.460, while that for behavior improved slightly from 0.445 to 0.450.
Here is the model output in an Amos graphic.
Summary
The structural equation modeling framework found in Amos enables you to use multiple indicators of your latent variables. The example above shows some of the benefits from SEM, including:
- Higher explained variance for endogenous variables (those with arrows flowing into them, such as intentions and behavior above)
- Disattenuated and statistically consistent estimates of structural parameters
- Estimates of the reliabilities of the measures, plus avoidance of the unrealistic assumption that your indicators are perfect measures
References
Bagozzi, R.P. 1996. Structural Equation Models in Marketing Research: Basic Principles, in Principles of Marketing Research. Richard Bagozzi (ed.), Cambridge: Blackwell Publishers.
Bollen, K. 1989. Structural Equations with Latent Variable. New York: John Wiley and Sons.